Allocation
Why randomisation needs to be used to allocate animals to experimental groups and how to generate a randomisation sequence.
- Why is randomisation important?
- What to randomise
- Choosing a randomisation strategy: complete randomisation or block randomisation?
- Ways to generate randomisation sequences
- Representing allocation in the EDA
- Using the EDA to generate a randomisation sequence
Why is randomisation important?
Allocation is the process by which experimental units are assigned to experimental groups. It can be achieved using various strategies for example a complete randomisation, a block randomisation or randomisation within matched pairs.
It is crucial that you carry out the allocation process using an appropriate strategy to prevent you from subconsciously influencing the allocation. However well-intentioned the experimenter is about not being biased, any process involving human judgement, including a ‘haphazard’ allocation, can never be truly random. This compromises the statistical validity of any results obtained. Systematic reviews have shown that such experiments are more likely to report statistically significant results, indicating that failure to properly randomise allocation of experimental units increases the risk of false positive results.
Randomisation is a process used to ensure that each experimental unit has an equal probability of receiving a particular treatment. Together with allocation concealment, randomisation helps minimise selection bias and reduce systematic differences in the characteristics of animals allocated to different treatment groups.
Whilst randomisation is specifically used to allocate experimental units to treatment groups, the principle is also relevant throughout the whole experiment. For example, animal cages should be housed in a random order on the shelves and all measurements should be done in a random order (preferably with the investigator also being blinded to the treatment received by each experimental unit).
What to randomise
In a situation where different groups of animals receive different doses of a systemic drug treatment, the experimental units (which are the animal in this case) are randomised into treatment groups.
In contrast, in a situation where the same group of animals is used to test several doses of a drug treatment, with a wash out period between each different dose, then each animal provides one experimental unit per test period. As the experimental units (an animal for one test period) are allocated into treatments, it is effectively the order of the treatments which is randomised to the animals.
Choosing a randomisation strategy: complete randomisation or block randomisation?
Experimental units can be allocated into treatment groups using a complete randomisation or a randomisation within blocks and/or factors.
A complete randomisation assumes that all animals are simultaneously randomised to the treatments without taking any other variable into account. In other words, the independent variable(s) of interest (i.e. treatment) are the only thing which might influence the outcome measure. This is rarely appropriate as in reality the result of an experiment can often be influenced by many variables. A complete randomisation would only be appropriate if the expected effect size is large and/or there is relatively low variability between animals of the same treatment group.
A randomisation within blocks uses at least one nuisance variable (i.e. source of variability that is not of interest but may affect the outcome) as a blocking factor. It can also be called restricted or stratified randomisation. Introducing a blocking factor essentially splits up the experiment into smaller sub-experiments – randomisation is then done within each of the categories of the blocking factor (i.e. each block). Ideally, each of the treatments should be administered in a balanced way within each block. The blocking factor should also be included in the analysis to reduce the unexplained variability within the groups. This increases the precision of the estimate of the effect of treatment, increasing the ability to detect a real effect with fewer experimental units. However, it is important to consider that blocking uses up degrees of freedom and thus reduces the power if the nuisance variable does not have a substantial impact on variability.
If animals with different characteristics are subjected to an intervention, and that characteristic is a factor of interest in the analysis, the randomisation strategy should be a randomisation within factors. For example, in an experiment looking for sex differences in response to a drug treatment, treatment groups should be balanced, with the same proportion of male and female animals.
Ways to generate randomisation sequences
Simple randomisation
For experiments with only two groups (e.g. control versus treatment), the simplest form of randomisation is to flip a coin to determine which group the animal is assigned to (i.e. head = control, tails = treatment). Simple randomisation can also be done by shuffling a pack of cards (red or black) or throwing a dice (odd or even). These simple methods work well for large groups but can be problematic in smaller groups where there is a greater risk of uneven numbers per group (unbalanced design) leading to reduced power – in this case the following methods can be used.
Spreadsheet generated by the EDA
The EDA can create a randomisation sequence for you when planning your experiment. The EDA randomises animals to groups based on both the number of animals and any additional factors in the experimental design – for example, a blocking factor or an independent variable of interest that needs to be randomised separately (e.g. sex). The randomisation sequence is generated as an Excel spreadsheet.
Computer generated
The function =Rand() in Excel can be used to generate a column of random numbers which you can use to randomly allocate animals to treatment groups. Consider for example an experiment with three treatment groups (1: control, 2: low dose and 3: high dose) with ten animals per group. Set up your Excel sheet as follows:
- Column A: =Rand() generated random numbers.
- Column B: Ten 1s, ten 2s and ten 3s (for each of the treatment groups).
- Column C: Unique identification numbers for each of the 30 animals.
Sorting columns A and B by the order of column A will randomise the order of column B, and each animal of column C will be allocated into treatment 1, 2 or 3 at random.
Numbers out of a hat
Ten 1s, ten 2s and ten 3s could be written on 30 pieces of paper which are folded and placed in a receptacle. After mixing, a paper is withdrawn and the first animal is assigned to the treatment number indicated, and so on.
Latin squares
Latin squares are useful to allocate experimental units to treatment groups in an experiment with two blocking factors, which are independent and have minimal interaction. Technically speaking, a Latin square is not a method of randomisation in itself but experimental units can be allocated to treatment groups via randomisation of a Latin square.
In a Latin square, the two blocking factors are defined by the rows and columns, the letters inside the cells represent the treatments. Below is an example of a 3 x 3 Latin square built using the cycling method:
|
Note that each treatment occurs only once per row and once per column. |
Example: crossover design
Latin squares are especially useful to balance the order of treatments in crossover experiments. A crossover design uses each animal as its own control, this accounts for the animal-to-animal variability which is typically the largest source of variability in animal studies.
Consider an experiment comparing the effect of two treatments (A and B) and a control (C) where each animal receives all three treatments, separated by a one week wash out period. This is effectively a design with two blocking factors – the animals and the test periods. The experimental unit is an animal for a test period and each animal provides three experimental units. Six animals are used in this experiment, bringing the total number of experimental units in the experiment to 18, with n=6 per treatment group.
The animal blocking factor is assigned to the columns, with the six categories forming six columns. The test period blocking factor is assigned to the rows, with the three categories forming three rows.
| Latin squares help you to randomise the order of treatments for each animal. Because there are twice as many animals as there are test periods and treatments, two colours of squares are needed (blue and green). | |
|
You must then randomise the rows and columns of the Latin squares to generate a random order of treatments across the three test periods for each animal. Thus, animal 1 will receive the control on the first week, treatment A on week 2 and treatment B on week 3. Animal 2 will receive treatment A, then the control, then treatment B, and so on.
|
Representing allocation in the EDA
In many experimental designs an initial group of animals is subjected to an allocation process, which produces several groups. The following diagram represents a pool group allocated into two groups. Further information about the randomisation strategy and procedure is added in the properties of the allocation node.
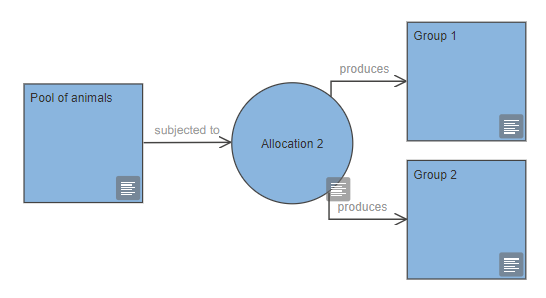
Blocking factors and animal characteristics that need to be allocated separately can be indicated on the diagram as in the image below. In the properties of the allocation node, the randomisation strategy can be described as a complete randomisation, a randomisation within blocks, within factors, or within blocks and factors.

Using the EDA to generate a randomisation sequence
Once you have planned your experiment in the EDA, you can generate the randomisation sequence that you will use to allocate animals to groups. In the window showing your experimental plan, go to the Tools menu and select Randomisation sequence. The EDA will then allocate animals into groups, creating an Excel spreadsheet containing the randomisation sequence.
If no blocking factors or factors of interest are connected to the allocation node, the sequence will be generated based on a complete randomisation. Any factors connected to the allocation node (including all variable categories, see image above), will be accounted for in the randomisation sequence.
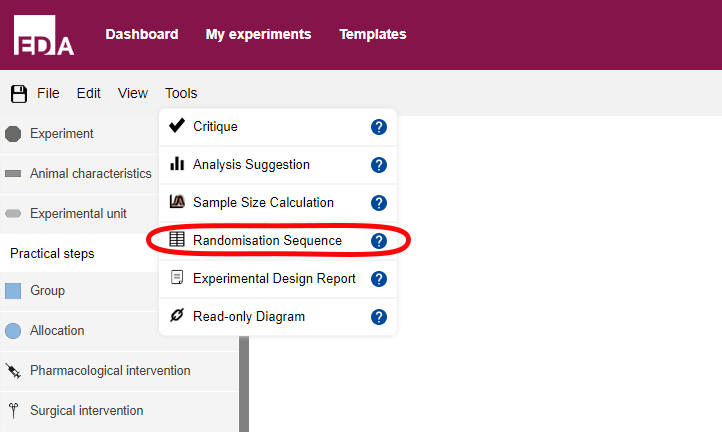
The randomisation sequence can also help you implement blinding (masking). The sequence can be emailed directly from the EDA to a colleague or collaborator, helping you to remain unaware of group allocations. For example, if the animals are subjected to a pharmacological intervention by injection you could have the randomisation sequence sent to the person who will be coding syringes for you. This way your entire experiment can be carried out with you unaware of the treatment(s) each animal has received.
Please note that in the current version of the EDA, the randomisation spreadsheet randomises animals into groups, based on the number of animals indicated in the properties of the groups produced by the allocation. In experiments where the experimental unit is not the individual animal, it may not be possible to use the allocation sequence generated by the EDA. The system only supports balanced designs, with groups of equal sizes and composition. For randomisation within blocks and/or factors the system may on occasion randomise more animals than indicated in the post-allocation groups to ensure that the same number of animals are included in each stratum.
References
Bate, ST and Clark, RA (2014). The Design and Statistical Analysis of Animal Experiments. Cambridge University Press.
Bebarta, V, Luyten, D and Heard, K (2003). Emergency medicine animal research: does use of randomization and blinding affect the results? Acad Emerg Med 10(6):684-7. doi: 10.1111/j.1553-2712.2003.tb00056.x
Festing, MFW, et al. (2002). The design of animal experiments: reducing the use of animals in research through better experimental design. Royal Society of Medicine.
Vesterinen, HM, et al. (2010). Improving the translational hit of experimental treatments in multiple sclerosis. Mult Scler 16(9):1044-55. doi: 10.1177/1352458510379612


